8.7 KiB
| layout | title | permalink | cardTitle | cardDesc |
|---|---|---|---|---|
| banner | Research | /research | Topics | We tackle a broad set of problems relating to electromagnetic phenomena, from classical extreme-scale modeling to electromagnetic information theory. |
Research Overview
The classical electromagnetic (EM) theory guided by Maxwell’s Equations has been around for over 150 years. It has an incredible impact on many modern technologies such as antennas and wireless communication, integrated circuits and computer technologies, remote sensing, lasers and optoelectronics, and more. Nowadays, with the exponential growth in computing power, machine intelligence and data revolution, quantum technologies and materials, there are enormous opportunities to continue advancing fundamental EM theories towards next-generation technology developments and applications.
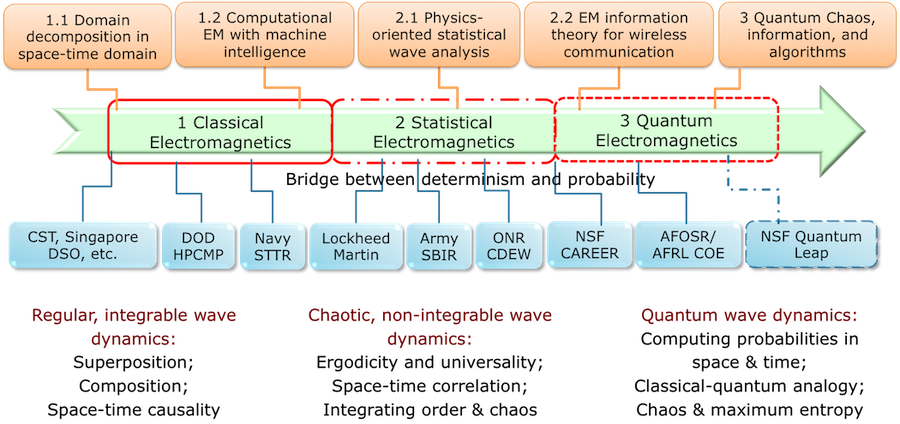
Our rudimentary research is the pursuit of mathematical and computational models that advance the understanding, prediction and discovery of classical, chaotic, and quantum wave phenomena. These models will allow for the design and optimization of novel electromagnetic systems at unprecedented scales, and contribute through education to the advancement of understanding. Our current and future research are concerned with four interrelated areas: (1) classical electromagnetism with scalable algorithms, (2) statistical electromagnetics: theories and practices, (3) quantum electromagnetics: simulating probability in space and time domain, and (4) chaotic reverberation chamber: measurement and control of uncertainties. The diagram of research roadmap and current supports is elaborated as:
Research Topics
Extreme-Scale Electromagnetic Modeling and Simulation in the Supercomputing Era
Collaborators: Ralf Hiptmair@ETH, Andrew Greenwood@AFRL
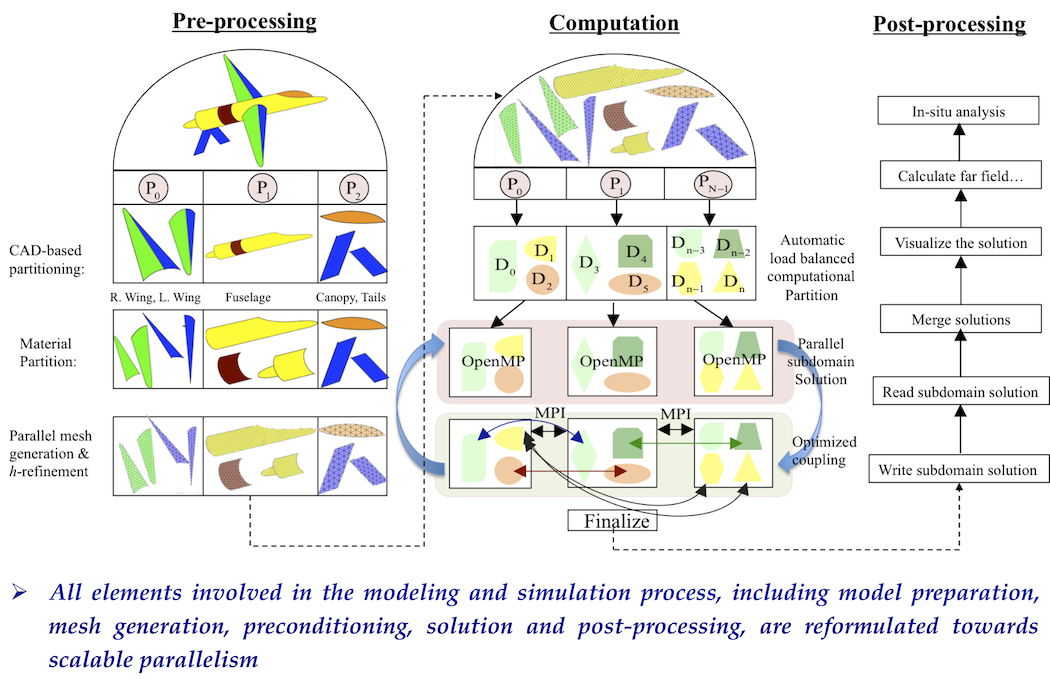
One basic research I have conducted is the pursuit of robust and yet efficient ways to solve Maxwell equations in their entirety. The research, usually called computational electromagnetics (CEM), is highly mathematical and abstract in itself, and can be stated as one of the principal research topics in electromagnetic fields. The implication and impact of this research is astronomical. It is the heart of modern computer-aided engineering/computer-aided design (CAE/CAD) tools for advanced antennas, radio frequency integrated circuits, electromagnetic interference and compatibility, signal and power integrity and other applications in electromagnetic and microwave engineering.
Ever-increasing fidelity and accuracy need for advanced EM applications have been pushing the problem sizestowards extreme scales. It puts a high premium on investigation of high-performance algorithms with optimal computational complexity. Moreover, increased demands are being placed on an integrated design andanalysis environment, which requires new simulation tools to be well integrated into design processes. Here,I briefly summarize my research contributions in the high-resolution and high-performance algorithms, whereboth simulation capability and modeling fidelity scale with the exponential growth in computing power.
 {:class="markdown-img"}
{:class="markdown-img"}
 {:class="markdown-img"}
{:class="markdown-img"}
 {:class="markdown-img"}
{:class="markdown-img"}
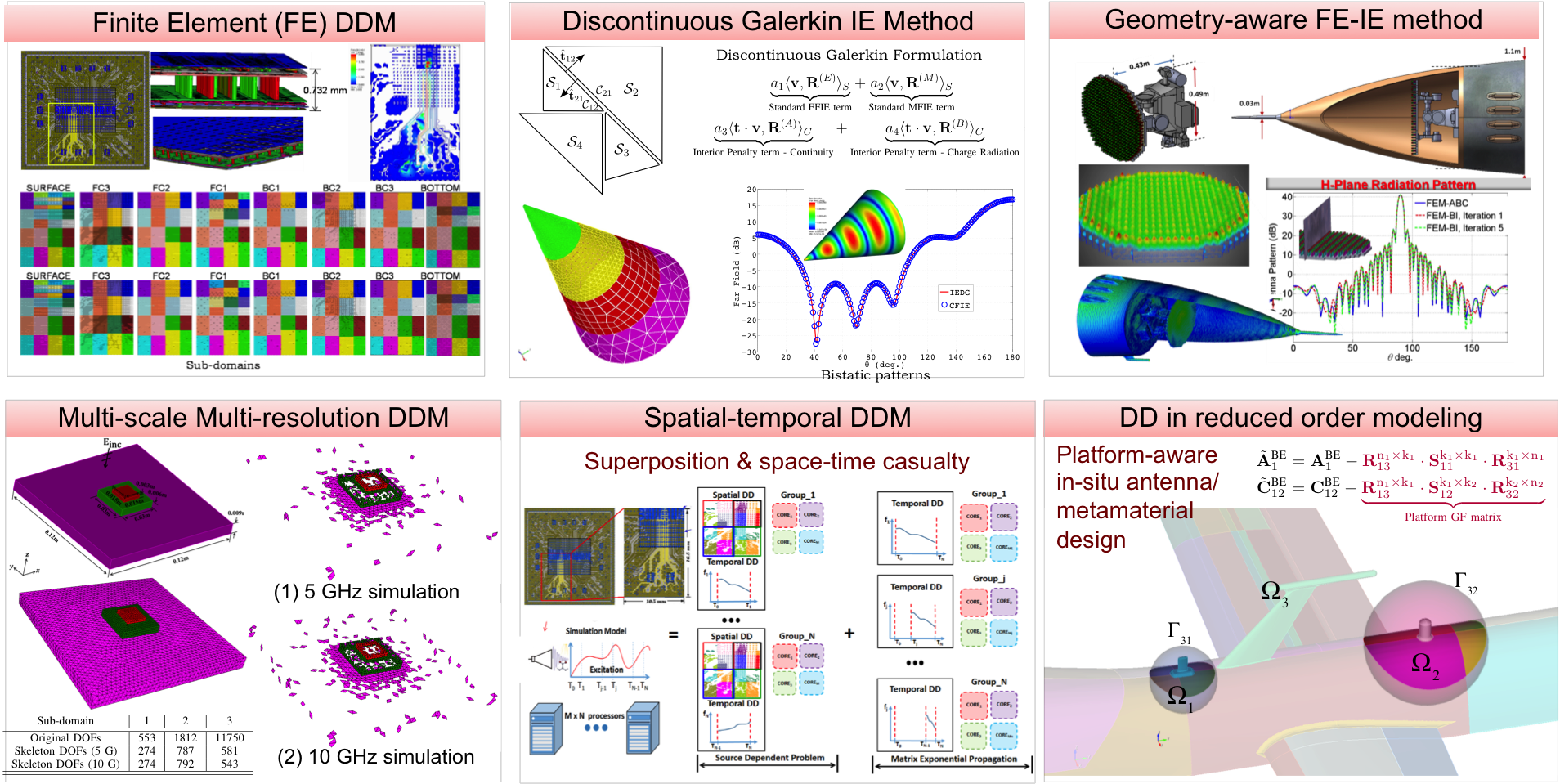
Domain Decomposition Methodology for Solving Maxwell's Equations
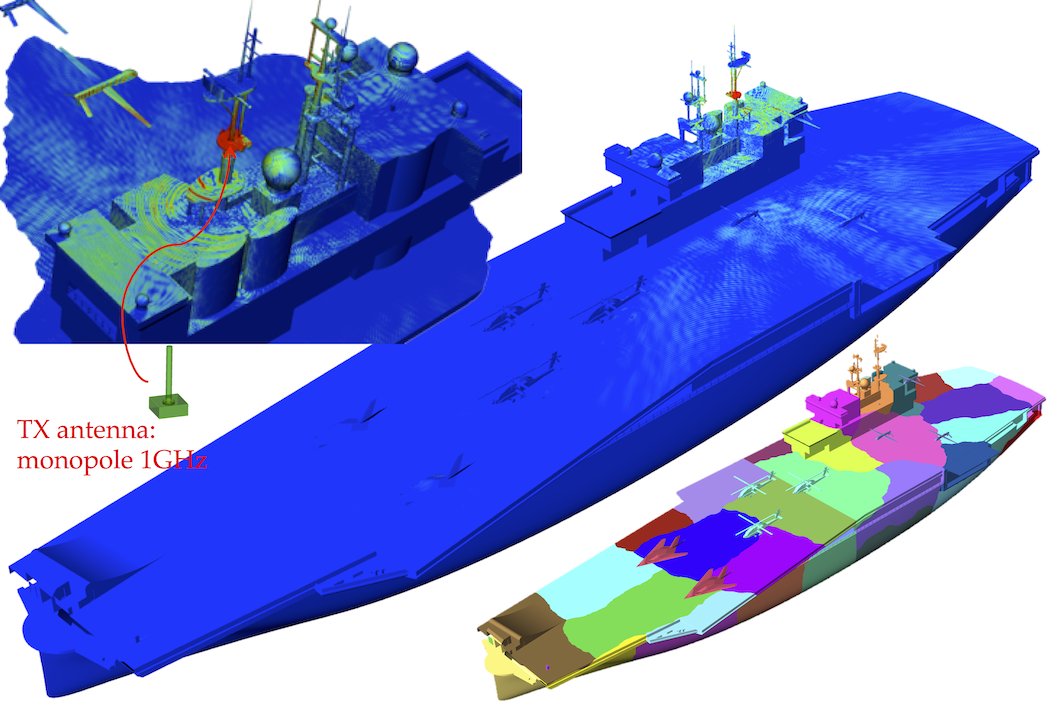
In recent years, domain decomposition (DD) methods have enjoyed considerable success in solving large multi-scale EM problems. These methods feature divide-and-conquerin solution algorithms (applying the most suitable solution strategy to solve each sub-problem) and plug-in-play in software architectures (integrating individual EM solvers into a portable and extensible solution suite). They also result in highly efficient and naturally parallelizable algorithms on distributed memory many-core parallel computing systems. We have been investigating novel DD algorithms for differential equations, integral equations, transient EM analysis, and reduced order modeling.
First-principles Electromagnetic Field-based Millimeter-Wave Channel Models
Collaborator: Christos Christodoulou@UNM
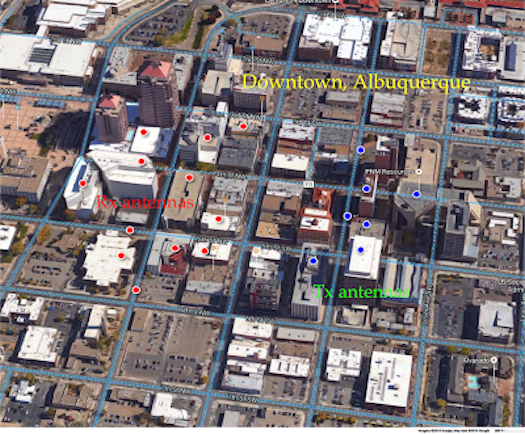
The objective of this work is to investigate a high-resolution and first-principles computationalmethodology for mmWave propagation channels in realistic usage scenarios. The work provides unprecedented resolution in deterministic channel modeling, andoffers a fundamental knowledge of mmWave channel characteristics and propagation behavior. Theadvancements are expected to initiate the transition from traditional ray-based high-frequency approximation to EM field-based full wave modeling methodology.
 {:class="markdown-img"}
{:class="markdown-img"}
 {:class="markdown-img"}
{:class="markdown-img"}
Physics-Oriented Statistical Wave Analysis Integrating Order and Chaos
Collaborators: Thomas Antonsen@UMD, Edl Schamiloglu@UNM, Sameer Hemmady@UNM)
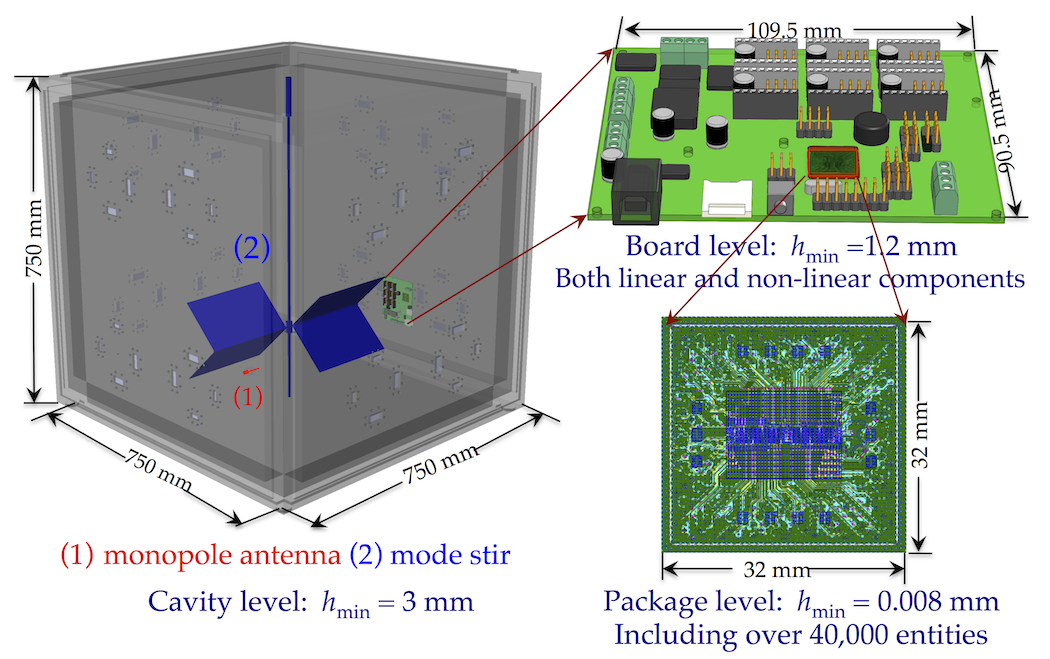
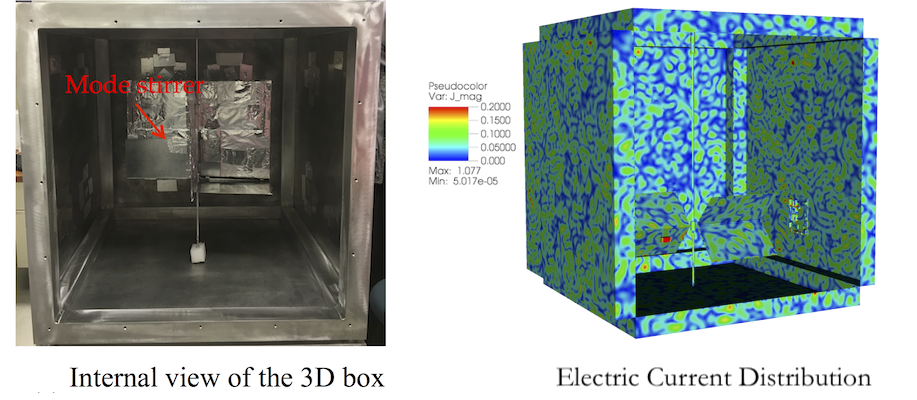
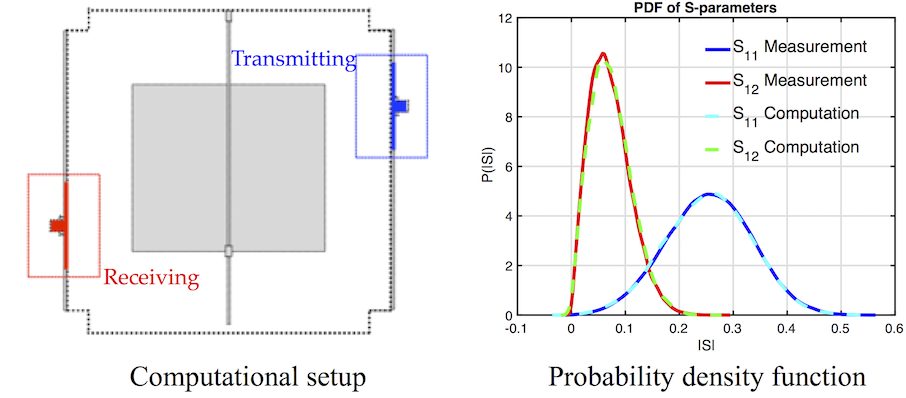
Even though we are seeking the highest possible fidelity, the computer representation will not be exactly the samecompared to the real world. These uncertainties may arise from imprecise knowledge of the system, small differencesin manufacturing, or numerical errors in the simulations. In integrable, regular wave systems, these small differencescan be considered as local perturbations of the entire system. Hence, the numerical solution is still a very goodapproximation to the exact solution of the physical problem. However, the situation can be completely different innon-integrable, wave-chaotic systems. The wave solutions can be extremely sensitive to details and initial conditions.It makes the traditional first-principles deterministic approaches relevant only to a specific realization.
This project investigates an innovative theoretical solution to Maxwell’s Equations in the wave chaotic (random,diffuse) media. The fundamental solution, named stochastic Green’s function, rigorously integrates the coherent andincoherent contributions within a unified compact form. Furthermore, by incorporating the component-, site-, system-specific information with the universal chaotic dynamics, the work accomplishes a comprehensive framework for thestatistical analysis and uncertainty quantification of complex wave systems. The advancements will achieve first-ever an imperative simulation-driven, design-under-chaos capability, and a virtual experimental facility statisticallyreplicating real-world wave propagation environments.
 {:class="markdown-img"}
{:class="markdown-img"}
 {:class="markdown-img"}
{:class="markdown-img"}
 {:class="markdown-img"}
{:class="markdown-img"}
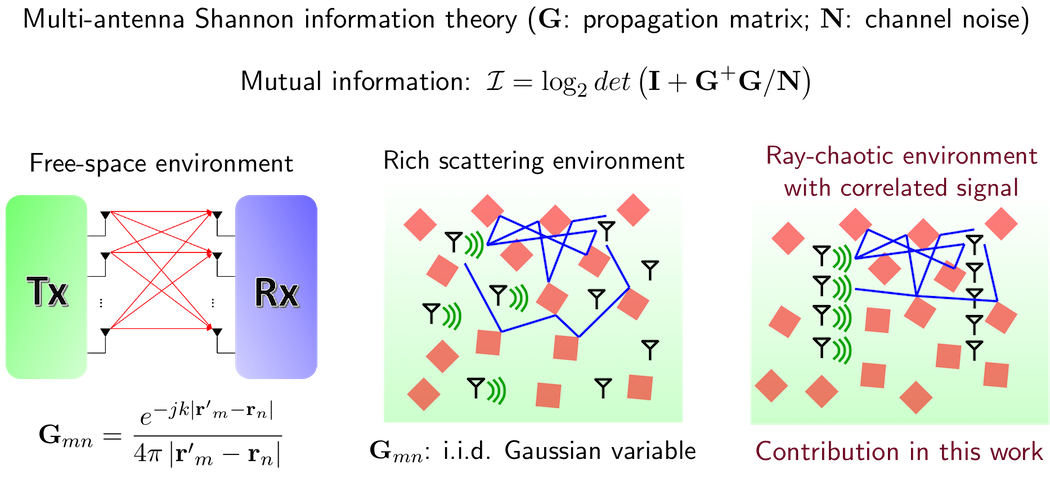
Electromagnetic Information Theory for Wireless Communication
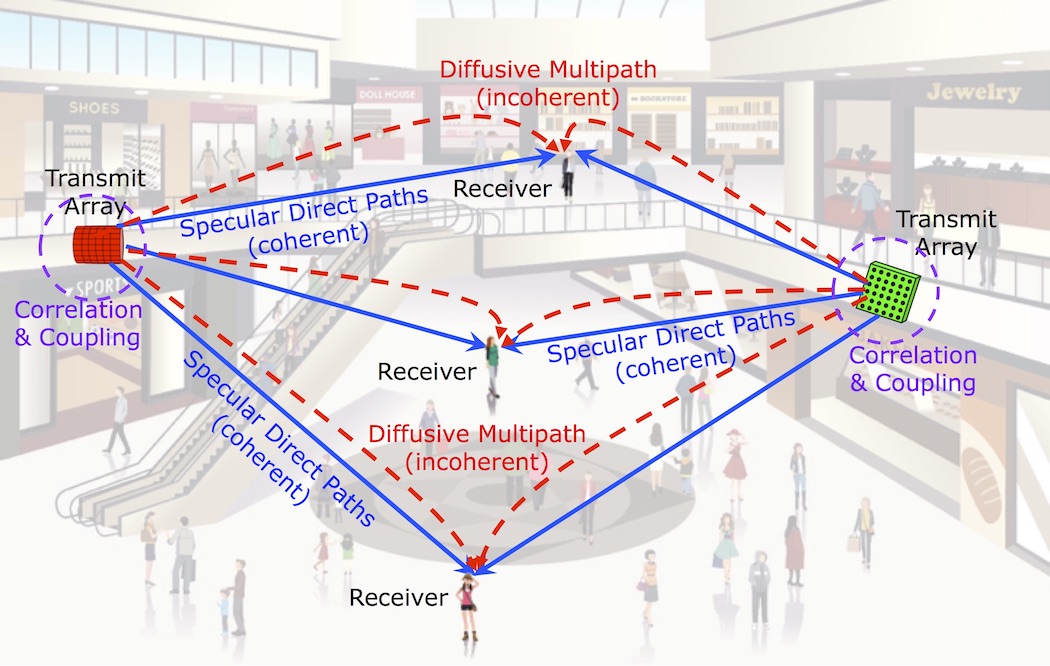
Electromagnetic field theory provides the fundamental physics of wireless communications. Over the pastdecades, EM theory has played a significant role in the design, performance assessment, and deployment planningof wireless devices and systems. Meanwhile, ever increasing demands for the network capacity in wirelesscommunications have pushed the data rate towards and beyond multi-Gigabits per second (Gbps). Massivedistributed arrays, mm-wave bands, network densification, and new waveforms serve as promising and powerfuloptions for achieving these rates. The major limiting factor preventing these emerging wireless systemsfrom realizing their full potential is our understanding of the physical layer. Specifically, our ability to preciselymodel the physics of wireless signal propagation channels in diverse and complex environments.
The objective of this research is to investigate electromagnetic information theory for wireless communication through complicated diffuse mulitpath environments. Applications include indoor radio channels,dense urban cells, transmission through diffusive random media and disordered media,etc. The objective is attained by cutting across traditional disciplinary boundaries between electromagnetictheory, wave chaos physics, random statistical analysis and information theory. The methodology is to firstestablish fundamental statistical representations of diffuse multipath media, then integrate component-specificfeatures of transmitters and receivers, and finally encode the governing physics into the mathematical information theory.